Knaldtech Start
User Tools
Sidebar
The Integrator
The Integrator is the interface that we use to adjust and refine the images that we create. Almost everything that is created within Knald needs to pass through it at some point and its settings can have a dramatic effect on almost all aspects of the program.
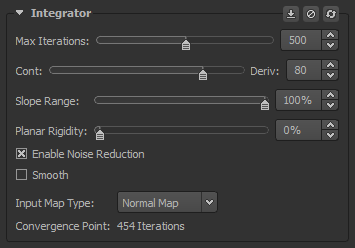
The Integrator Group's Settings
Max Iterations: The maximum possible number of iterations that the integrator will use when processing. It should be noted that this setting does not specify the exact number of iterations used, as the integrator will automatically try to find the best value which will be displayed under the Convergence Point field, but only the maximum amount of iterations that you want to be used during processing.
Cont/Deriv: This slider provides a balance between the preservation of continuity between the values of any given pixel and its neighbours and the conservation of the slope of a surface which is the derivative. The closer the slider is towards Cont:, the more continuous the values found in the resulting height map will be, whereas the closer the slider is moved towards Deriv:, the more accurately the slopes will be preserved at the expense of continuity between pixel values.
- We do not recommend going above a value of 90 as this can cause noise to appear in the map.
- A value of 80 should be perfect for most situations.
Slope Range: This slider increases the permitted range for slopes in the Normal & Derivative maps which can substantially increase the accurateness of the Integrator.
- This should be used with caution! Results may vary and can depend greatly on the quality of the imported image.
Planar Rigidity: This slider is used to preserve the flatness of an imported texture and to get more consistently even values in the integrated Height map.
Enable Noise Reduction: This check box is a toggle to enable and disable noise reduction before the texture is processed through the Integrator.
Smooth: This check box is a toggle to enable and disable the smooth function before the texture is processed through the Integrator.
Normal Map/Deriv Map: The type of input used for the integrator.
Convergence Point: The best iterations value found automatically by Knald after processing an image.
